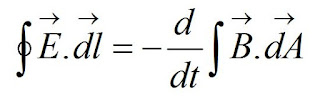To do Faraday's Law at school I put a magnet inside a coil of wire attached to a millivoltmeter. When the magnet was pulled out slowly this is the reading I got today:
Then I pulled it out fast and got
Faraday's Law says that the induced emf (the voltage shown on the meter) is proportional to the rate of change of flux linkage. The faster I pull the magnet, the bigger the rate and the bigger the emf. We write it like this
the fancy E is the emf and the Greek letter phi is the magnetic flux - the field lines that are often shown using iron filings.
Looking in a degree level text book, this is written in Maxwell's equations as
E is the electric field strength, which is the same as force per unit charge, F/Q. The fancy signs mean a line integral. You add up E x a small distance dl all the way round a loop. E x length is the same as F/Q x length but F x length is work done. So the expression on the left if work done W divided by charge Q. W/Q is voltage - so that's my emf. B is the magnetic flux density. It is multiplied by small areas dA and they are all added up. But B x area = magnetic flux phi. The line integral on the left is for one circuit of the loop. One loop means N = 1. So I have figured out how to get the hideous degree level equation back down to the one I use all the time.