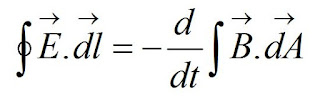U-tube came before YouTube

Seen in the hands of Joseph Black in the portrait gallery in Edinburgh ... This piece of equipment is why the name of the video channel on the Internet is a clever physics joke for those in the know. A u-tube usually contains a fluid like water. It can be used as a manometer to measure gas pressure by connecting one end of the u-tube to the gas and leaving the other end open to the atmosphere. If the gas has a pressure higher than that of the atmosphere, the liquid moves round to the atmosphere side. Vice versa if the situation is reversed. Or a u-tube of water with nothing attached can be shown to exhibit simple harmonic motion if the water is displaced to one side and allowed to oscillate.

Sixth Form Question: How big is the Moon's orbit

1. Make measurements on yourself to show that an outstretched finger subtends roughly 1 degree (ie the angle for an isosceles triangle staring at the left end of your outstretched little finger, coming in to a point at your eye and going back out to the right hand aide of your little finger).
2. The Moon is shown in the picture along with my little finger. Compare the two and use it to work out the angle subtended by the Moon.
3. The diameter of the Moon is given as 3474km. Use this and your answer to Q2 to work out the radius of orbit of the Moon around the Earth.
4. Find the true value for the radius of orbit of the Moon and calculate the percentage difference in your answer.
5. State and explain one false assumption that we have made.

Homage to Maxwell in Edinburgh

Imagine my joy on coming upon this statue of James Clerk Maxwell in the middle of Edinburgh. I'm so impressed that they have put his equations into the pavement like a work of art. The upside down triangle is called del or nabla. It is a method of differentiating a vector field (ie a series of arrows like a map of wind speeds) that exists in three dimensions. The differentiation means finding a gradient. The dot means finding the gradient along the line of one of the vectors. The cross means in a direction perpendicular to both of the vectors. These four equations sum up all of electromagnetism and he used them to predict the existence of electromagnetic waves, figuring out that light must be one when his theoretically derived speed turned out to be the speed of light.

Total internal reflection in the fish tank

I have often taught about total internal reflection and explained that if you were underwater in a swimming pool, you would be able to see the pool floor reflected by the water surface above you. I've never been able to photograph it because my camera isn't waterproof. So here's TIR at Matryport Aquarium. I was surprised because the whole surface seemed to act like a mirror. If you are underwater in a pool and look straight above you, in theory there shouldn't be TIR because the light doesn't bend. That didn't seem to be the case no matter how close I put my head to the glass. Maybe that was due to refraction in the glass. The glass walls of the tank seemed weird.

Haweswater Hotel: Threshold values

Threshold values occur a lot in science but these days few of my students know what a threshold is. Here it is in the photos: a doorstep. It is the entrance - in science it is the value at which something starts - just as if you were going into the house. An example would be the threshold frequency for the photoelectric effect. Above a certain frequency, any light shone on a metal will release electrons from the surface which can allow a current to flow across a specially designed gap in the circuit. Below that frequency, no electrons are released and nothing happens. So that frequency is the threshold frequency. Go beyond it and the action starts.

Mackeral sky and the breaking up of a contrail

Here is a mackeral. Look at the stripes on its side. No wonder mackeral sky gets its name.

Look at the aeroplane vapour trail above Harter Fell at Mardale.

Some time later the trail had broken up. It broke up into mackeral sky. A lateral wind has spread the trail sideways thickening the trail but it has banded along its line. I will need to see if this is frequent.

The Bowder Stone

I'm always a sucker for notice boards like this. The volume measured in "solid feet" caught my eye. How can we model the volume from the data for such an irregular shaped block? Given the circumference and perpendicular height, I have decided to try using a cylinder. Circumference = 2*pi*radius. So radius = 89/2*pi = 14.1 feet. Area = pi*radius-squared = 630 square feet. Volume = area x height = 22691 cubic feet, to too many sig figs. Almost right. An Internet conversion device gives the value mentioned on the board as 651 cubic metres. In the old UK measures, there were 20 hundredweight (cwt) in a ton.So there were 1971.65 tons. This is 1971.65 x 1016.047 = 2.003 million kg. The density of the rock is therefore = 2.003 million/651 = 3077 kg per cubic metres. Try an Internet search for porphyritic greenstone. It seems to come up in very ancient references from about the date of this notice. But the density is right for the top end of basalt. It should be too high for granite. It also seems too high for andesite which is the most common rock type I come across.

U values in the snow at Stonethwaite

I spotted this in Stonethwaite at the end of Borrowdale. Why has the snow fallen from the window but not from the roof? I remembered this table of U-values:

Rate of heat loss from a building = area x U-value x temperature difference.
The bigger the U-value, the faster the heat is lost. Even double glazing has a bigger U-value than an insulated roof so the window will have been leaking thermal energy more effectively hence the snow has melted.

Why the curl formula produces circulation

Working in the xy-plane (ie in an attempt to work in 2D) the curl equation becomes

I set out to work out what this actually means. I drew a vector field of parallel vectors heading up from bottom left to top right and increasing in magnitude in a uniform manner.

 In the bottom right hand corner of the picture above I have shown that each vector F made up of an x-component Fx and a y component Fy. On the diagram below I have shown how the size of those y component changes as you head out along the x-axis and how the size of the x component changes as you head up the y-axis. The first term in the top equation tells you the rate at which the y component increases as you go along the x-axis. The second term is the rate of increase of the size of the x component with increase in y. If the x and y components increase at the same rate, the vectors will continue to point along their straight slanted line. The equation will give an overall value of zero. If the y component increases at a faster rate that the x component, the arrows would tend to become more vertical as they go from bottom left to top right. The line of vectors will twist and the top equation will give a positive value. The y components twisting in an anticlockwise direction will tend to beat the clockwise x components. The twist will be anticlockwise. It fits with the right hand grip rule. I think this is the meaning of the curl equation.

Thinking about curl in the cafe at Maryport Aquarium

The log burner in the cafe at Maryport Aquarium had a fan on top. I've never seen a device like it. I had hoped it was being driven by the hot air rising from the stove but there was a wire on the back...
Unplugged, such a paddle wheel would be a means of determining whether or not a vector field has curl. Without a battery, this wheel will only turn if the upwards flow of air on one side is stronger than the upwards flow of air on the other. If that is true, then the vector field for air flow above the stove will have the property called curl.

Green's Theorem

 George Green was a brilliant mathematician who also operated a windmill in Nottingham. I used to cycle past it almost every day. I never understood what his big trick was. I think I've got it at last. It is to do with vector fields. An example of a vector field is a wind speed weather map. It is a series of straight arrows drawn on the map showing the direction of the wind and the length of the arrow representing wind strength. Entry-level differentiation is a mathematical trick to find the gradient of a graph. But how do you differentiate a set of arrows? There are two techniques which might have something to do with vectors having size and direction. These techniques are call div (divergence) and curl. Curl turns out to be the circulation per unit area of the fluid or whatever else is modeled by the vector field. I've drawn a lot of mini circulations inside the Helmholtz coil shown above. To find the actual circulation, we need to do the curl of the function (let's call it F for field) and multiply it be the tiny area because curl is circulation per unit area. So each square above represents a circulation curl F x dA. If we add them all up we get the total circulation. But look at the picture below. At each internal boundary the flow is equal and opposite and thus cancels. Adding up all the circulation elements just gives you the large total flow, shown by the outer red arrow in the top picture. Green showed that this outer flow could be found by adding up tiny sections of the line denoted dl multiplied by the function F. Thus adding up F.dl all the way round a curved line equals adding up all the curlF x dA across an area. He links function F round a circular line with the curl of F across an area inside this curve. This can be useful trick to swap between lines and areas

How to get Maxwell's Equation from Faraday's Law

To do Faraday's Law at school I put a magnet inside a coil of wire attached to a millivoltmeter. When the magnet was pulled out slowly this is the reading I got today:

Then I pulled it out fast and got

Faraday's Law says that the induced emf (the voltage shown on the meter) is proportional to the rate of change of flux linkage. The faster I pull the magnet, the bigger the rate and the bigger the emf. We write it like this

the fancy E is the emf and the Greek letter phi is the magnetic flux - the field lines that are often shown using iron filings.
Looking in a degree level text book, this is written in Maxwell's equations as

E is the electric field strength, which is the same as force per unit charge, F/Q. The fancy signs mean a line integral. You add up E x a small distance dl all the way round a loop. E x length is the same as F/Q x length but F x length is work done. So the expression on the left if work done W divided by charge Q. W/Q is voltage - so that's my emf. B is the magnetic flux density. It is multiplied by small areas dA and they are all added up. But B x area = magnetic flux phi. The line integral on the left is for one circuit of the loop. One loop means N = 1. So I have figured out how to get the hideous degree level equation back down to the one I use all the time.

A claim about raging rivers

We found this display at Maryport aquarium. I was struggling with how to work this out. Once source I found even says the claim is erroneous. I knew I was starting with momentum change but couldn't get the 64 factor. Apparently it is the Sixth Power Law, that mass of object goes with the sixth power of velocity. 2^6 = 64. This source gives a way of getting it: https://physics.stackexchange.com/questions/132620/sixth-power-law

Dead spot in the fish tank in Maryport

In the aquarium at Maryport there is a fish tank with a spherical viewing cavity that you can crawl into. The picture above shows from the outside through the fish and then the cavity. I crawled in. There was the odd sensation of being able to hear in one ear and not the other. I moved around. It became apparent that there was an acoustic dead spot. My first thought was that it would be a node on a stationary wave set up inside. Thinking about it later, it occurred to me that the dead spot was almost where you'd expect the focal region of a spherical mirror to occur. But that should be loud not quiet. I'll try to take a tape measure next time I go to get some better data. Below is the view from the inside looking out.

Old crash barriers in Kidlington

I investigated the new style crash barriers in the summer and learned that they had replaced this type. These ones have the end bent down into the ground to stop the end piercing the body of the car in the collision. The problem with this design turned out to be that it added a vertical component to the force applied to the car because the normal contact force is pointing up an angle 90 degrees to the inclined surface of the barrier. This will cause a vertical component to the resultant force on the car, thus an upward acceleration and it will make a car flip if the car hits at the wrong angle.

Atholl Hydro on the A9

http://www.gilkesenergy.com/project/Broom I spotted this beside the A9 and looked up the data. It says it can shift 400 litres per second, which is 400 kg per second. The head is 163m. So say that 400kg falls through 163 metres. It loses 400 x 9.81 x 163 = 639kJ of gravitational potential energy. I'm tempted to say that this equate to 639kW because of the per second bit but am mindful that it must take longer than 1 second to fall down the 2km pipe. On the other hand, this may be confusing energy and forces methods. It can operate at 483kW which would give an efficiency of 76%. Need to think about this one.

Radial tyres on the M74

This was the scene on the M74 heading north. If a layer of water gets between the rubber and the road, brakes will stop the wheels rotating but the water will act as lubricant and allow the rubber to slide along. This lack of friction is called aquaplaning. On a molecular level it will be to do with the fact that water molecules have only weak bonds between them so are subject top shear forces, tearing forces that allow layers to slide over one another. good radial tyres allow water to flow out through the valleys in the tread. You can see on the road surface where tyres have dispersed the water leaving clear tracks.

Room as echo chamber

This bedroom was particularly noisy. Thin walls and creaky floorboards. It seemed you could hear everything that was being said in the neighbouring rooms. So was the room acting as a resonating chamber, a sound box. It was about 4 metres long. For a stationary wave with a node at each wall, that would mean a wavelength of 8 metres. Frequency = speed of sound/wavelength = 340/8 = 43 Hz. Even for a male voice, this would be a bit low. On the other hand, 100Hz might just hit the second harmonic!

Surface area to volume ratio: Snow Buntings at Cairn Gorm

The Snow Bunting was much bigger than I expected when seen close up. Size matters. Volume contains cells that generate thermal energy. The bigger the volume, the more warmth for polar species. Thermal energy is lost through the surface. Consider a sphere. Volume = 4/3 * pi * r^3. Surface area = 4*pi*r^2. Hence if I double the radius, volume is up by a factor of 8 whilst surface area is up by a factor of 4. 8x the thermal energy generated but only 4x the rate of heat loss. So it pays to be big to stay warm.