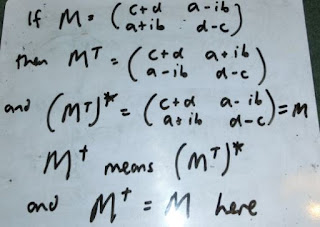Friday, 30 November 2018
"Deep time" at Red Wharf Bay
In his introduction to the re-print of Clarence Ellis's book The Pebbles on the Beach, Robert Macfarlane says that geology gives him a sense of what he calls "deep time". Ellis was born on Anglesey and it was on Anglesey that I got the sense of "deep time". We found these alternating layers of limestone and sandstone. The former was laid down in tropical seas and then the land rose, leaving rivers to deposit the sand and swamps the black mud shale deposits. Human history goes back in the thousands of years but I get the impression that each layer must represent a time longer than that. I'd be interested in finding out how long a time each layer represents and how you would work it out.
Thursday, 29 November 2018
Getting an IV characteristic for a red LED
We used a potential divider to change the potential difference across a red LED. We measured the current through it for each voltage. To obtain negative voltages, we swapped the connections round on the power supply.
The graph looks like this:
There is no light for negative voltages but even with positive voltages, nothing happens until around 0.7V and even then we were getting current of 0.02A with 1.5V.
The graph looks like this:
There is no light for negative voltages but even with positive voltages, nothing happens until around 0.7V and even then we were getting current of 0.02A with 1.5V.
Wednesday, 28 November 2018
Contact resistance
We were doing an experiment to find the EMF and internal resistance of a cell by clipping in different sizes of resistor. The idea is that the resistance changes the current and the current heats the internal resistance, changing the output p.d. If you plot output p.d.against current, the y-intercept is the EMF and the internal resistance is - gradient. But with the 1 Ohm resistor I was asked if the direction of the resistor affected the current like it would with a diode.
The answer is that it doesn't, but that there is extra resistance added into the circuit by the way that the clips grip the wire. It is unavoidable and changes in size every time you reattach, hence the seemingly different reading. It is a small resistance but might be a reasonable fraction of 1 Ohm and thus affect the current readings for very small resistances.
The answer is that it doesn't, but that there is extra resistance added into the circuit by the way that the clips grip the wire. It is unavoidable and changes in size every time you reattach, hence the seemingly different reading. It is a small resistance but might be a reasonable fraction of 1 Ohm and thus affect the current readings for very small resistances.
Monday, 26 November 2018
A simple cell
We made simple cells by soaking filter paper in a strong brine solution and connecting up two metals of differing reactivity on either side of the paper. Here we had nickel and copper. I'm working on an explanation as to how the differing reactions mean that more electrons are pushed by one side than by the other.
Sunday, 25 November 2018
Wind in the wire: Abergwyngregyn
It was a windy day when we walked under the wires and there was a steady roar that I worked out was the sound of the wind in the wires. I'll estimate 100Hz. Let's assume that it has set up the first harmonic of a stationary wave. The equation for calculating the frequency is:
Where L is the length of the wire (1000m as measured on the map), T is the tension of the wire and mu is the mass per metre. The wire is aluminium with steel core. Let's round up the density of aluminium to 3000 kg per cubic metre and estimate circular cross-section of 4cm diameter. Cross-sectional area = 0.001 square metres and mass per unit length of 3kg. That would give a tension of 120 billion Newtons. Breaking stress for the steel is 7.9 x 10^8 Newtons per square metre. This figure would exceed that so some of my estimates or assumptions must be wrong.
Where L is the length of the wire (1000m as measured on the map), T is the tension of the wire and mu is the mass per metre. The wire is aluminium with steel core. Let's round up the density of aluminium to 3000 kg per cubic metre and estimate circular cross-section of 4cm diameter. Cross-sectional area = 0.001 square metres and mass per unit length of 3kg. That would give a tension of 120 billion Newtons. Breaking stress for the steel is 7.9 x 10^8 Newtons per square metre. This figure would exceed that so some of my estimates or assumptions must be wrong.
Saturday, 24 November 2018
Diffraction at RSPB Conwy
This was going to be a piece about how the ripples on the water help us to see the invisible gusts of wind. Each gust sent a set of short wavelength ripples across the surface - an interesting real-time visualisation tool. But it didn't photograph well. However, I did notice that as well as the high frequency noise on the surface, there were also lower frequency waves crossing the pond.You can see them in the clearer water beneath the clump of reeds in the water in the middle of the picture. Why are they suddenly visible there? The answer seems to be that their wavelength is closer to the size of the clump so they are able to bend into the sheltered space behind the clump by diffraction. The much shorter wavelength noise isn't able to diffract and so goes straight past.
Friday, 23 November 2018
Variable resistor controlling a bulb
Here we took a rheostat that has 3 terminals and only connected 2 to make a variable resistor. Above, the variable resistor is set to zero so that all of the potential difference is across the bulb. But below, the variable resistor is on its highest resistance setting. You can tell because the current reading in the left hand meter has gone down. There is still a potential difference across the bulb, shown by the other meter. The bulb is off so you would have though that the potential difference would be zero. That's the problem with a variable resistor as a way of controlling a bulb. No matter what you do, the potential difference of the bulb will never go down to zero. If you want that when, for example, doing IV characteristics, you have to connect up all 3 terminals to wire the rheostat up as a potentiometer.
Thursday, 22 November 2018
Short circuit
We set up a circuit with two bulbs in it. The ammeter reading was 1.00A. Note that I'm holding a spare unconnected lead.
Then the lead was connected to the other side of the bulb. That bulb went out straight away and the current went up to 1.39A. The spare wire is called a SHORT CIRCUIT. The increased current can be dangerous because current is what heats in a circuit. The extra heat can sometimes set fire to the insulation and cause house fires.
Then the lead was connected to the other side of the bulb. That bulb went out straight away and the current went up to 1.39A. The spare wire is called a SHORT CIRCUIT. The increased current can be dangerous because current is what heats in a circuit. The extra heat can sometimes set fire to the insulation and cause house fires.
Wednesday, 21 November 2018
Interesting design of car park light at Dobies
This design of light is at Dobies at Dalston. It seems to be designed to reduce light pollution. All of the light should be directed downwards. The silvered surfaces are also dimpled. I assume this is the ensure diffuse reflection so that an image is not focused anywhere below.
Monday, 19 November 2018
Thermistor experiment
Today we put a thermistor into hot water with a thermometer and watched the resistance as the water cooled down. The resistance went up. I now understand the band theory idea better after learning some solid state quantum mechanics. Single atoms have clearly defined electron energy levels but as you bring atoms closer together to bond them, the electron energy levels cannot merge. Instead, for neighbouring atoms, one has its level nudge slightly up and the other has it nudge slightly down. On a grand scale, this results in a lot of almost but not quite identical electron energy levels. They form bands because they are grouped around the same energy. In semi-conductors, there is a clear gap between the valence band for bonding and the conduction band. Thermal energy is enough to move some electrons up from the valence band to the conduction band. More conduction electrons means higher current so we conclude that the resistance has fallen. The converse is true for cooling.
Sunday, 18 November 2018
Shadows in the sky
In the picture above, there is a thin dark band stretching down and right from the edge of the cloud. It is a shadow of the cloud as the Sun was away over to the left at the correct angle. Consider the photograph below. The shadow appears on the solid surface. There is no evident shadow visible in the air between us and the concrete. I have seen higher clouds project shadows onto lower levels so it suggests that tenuous water vapour in the air above the Solway might be substantive enough to scatter light from the Sun back to us, making it obvious where there is no light getting through to be scattered. It's like seeing a shadow projected onto smoke.
Sunday, 11 November 2018
Considering eigenvalues and eigenvectors
I'm reading this wonderful book again. I have been stuck for a long time trying to get an understanding of what a state actually means in Quantum Mechanics. I started with eigenvalues and eigenvectors for spin. If the spin operator acts on |u> then it remains unchanged. So |u> is an eigenvector. The eigenvalue is the multiplier - in this case it is +1. Notice that applied to |d> you get the same vector |d> but multiplied by -1. So |d> is an eigenvector with eigenvalue -1. The significance of the eigenvalues is that whatever state the system is in, you only ever measure it out as +1 or -1. So I picked another state vector and multiplied it out. I showed that it could be written in terms of the eigenvectors |u> and |d>. However if the system is in this mixed up state and you measure, you still get either +1 or -1. These are the eigenvalues. I have been wondering what the significance of the eigenvectors are.
Susskind says that this component state vector tells us the probability of measuring +1 or -1. I experimented myself with the maths, so what is below might be wrong but I think that the expectation value is the inner product squared. I get a probability of 1/2 which is what I expected. I think I have uncovered the significance of the orthogonal basis. The zero result for removes it from the equation. Orthogonal products give either 1 or 0.
Susskind says that this component state vector tells us the probability of measuring +1 or -1. I experimented myself with the maths, so what is below might be wrong but I think that the expectation value is the inner product squared. I get a probability of 1/2 which is what I expected. I think I have uncovered the significance of the orthogonal basis. The zero result for removes it from the equation. Orthogonal products give either 1 or 0.
I have struggled with degenerate states. Different eigenvectors but with the same eigenvalue. So only one value is measured. The eigenvectors are not orthogonal but you can construct an orthogonal basis by putting together linear combinations of them. I am trying to get this in writing whilst I am thinking about it and may have to publish corrections later.
Saturday, 10 November 2018
Maths on In Our Time
Melvyn Bragg is Lord Bragg of Wigton and through his Radio 4 programme In Our Time has been a great friend of Physics. Recently I have been enjoying back issues on Maths. Try these: https://www.bbc.co.uk/programmes/b09gbnfj and https://www.bbc.co.uk/programmes/b00dshx3 I have been trying to learn about Hilbert Spaces to understand Quantum Mechanics and the second programme gave me an insight into Hilbert's character.
Thursday, 8 November 2018
Learning about Hemititian Hamiltonians
Today I have learned that a Hermitian matrix like a Hamiltonian is real on its diagonal but has complex conjugates the other way. Leonard Susskind says that any operator L can be made up up components of the spin operators and the identity. a, b, c and d are real.
Dagger means the complex conjugate of the transpose. I then did an example with numbers.
Wednesday, 7 November 2018
Bradwell: First nuclear power station to be decommissioned
We went to see the war memorial at the former RAF Bradwell in Essex. The site became a nuclear power station after the war. It was the first in the UK to be decommissioned, being turned off in 1962. It generated 242MW across two units. There are now onshore wind farms that can generate as much as one of those units, but not with the continuity or compactness of supply. https://en.wikipedia.org/wiki/Bradwell_nuclear_power_station https://en.wikipedia.org/wiki/Arecleoch_Wind_Farm
Sunday, 4 November 2018
Diffraction grating net curtain
Here is the light reflected from a car through a lace curtain. The cross shape is the result of diffraction by the horizontal and vertical fibres.
The pattern is roughly 1 degree wide. I could see two orders of fringes on either side of the central maximum. Red was the furthest out and violet closest to the centre.
The pattern is roughly 1 degree wide. I could see two orders of fringes on either side of the central maximum. Red was the furthest out and violet closest to the centre.
I examined the weave with a magnifying glass and a ruler. There were approximately 4 holes per mm. Using the equation n.lamda = d.sin(theta), then d is approx 0.25mm. For first order fringe, n=1 and theta will be about 0.25 of a degree. That would give a wavelength of about 1000nm to 1 sig fig. That is very close to the range for visible light of 300 - 700nm. Not bad for a ruler and a little finger.
Saturday, 3 November 2018
Handleless coffee cup
I was a little bit perturbed to be handed what looked like a glass of hot coffee but it turns out that the bottom of the cup is a double layer of plastic trapping air. The trapped air is a good insulator because the air molecules are not joined together - they are actually quite far apart - meaning it is hard to pass extra kinetic energy one to another. Trapping it means that energy transfer by convection is also prevented. Reduced heat flow means that the outside is cool enough to grip safely.
Friday, 2 November 2018
Magnetic attraction weakens with separation
I got this experiment from an exam question. I taped a 0-10N spring balance to a bar magnet and had it attract a second bar magnet. I measured the force needed to pull them apart. Then I added card between the magnets and measured the force again. It took about 4 bits of card until the force of attraction between the magnets was too weak to measure.
Thursday, 1 November 2018
Brillouin-Wigner perturbation theory part 2
What I'm doing here is trying to do the workings to prove the results in the document linked to yesterday's post -seeing if I can follow the workings and understand it.
First we add a perturbation to the original Hamiltonian Ho. Most other methods I've seen use V instead of H1 because the perturbation is thought to be a potential energy from some external field.
Now here I have one problem. I thought En was a number - an eigenvalue that tells us the measurable energy - but it is having the original Hamiltonian Ho subtracted from it. Perhaps it is En x identity matrix. We had something similar in yesterday's workings where the Hamiltonian was given as the sum of eigenvalues En x Pn. Pn is a matrix. He does say at the top of the document that the curly small Es are eigenvalues and En is distinct so my hunch may well be correct.
Again below I'm not quite sure where the Pn in the summation for Ho on the bottom disappears to.
I can follow this bit. It assumes that perturbed and unperturbed eigenkets are in the same direction, but I think that is the idea with the small perturbation. The energy values change but not the ket direction.
So we finally get to write perturbed state in terms of the unperturbed, which confirms my last comment.
More maths to follow to work out the perturbed energies En.
First we add a perturbation to the original Hamiltonian Ho. Most other methods I've seen use V instead of H1 because the perturbation is thought to be a potential energy from some external field.
Now here I have one problem. I thought En was a number - an eigenvalue that tells us the measurable energy - but it is having the original Hamiltonian Ho subtracted from it. Perhaps it is En x identity matrix. We had something similar in yesterday's workings where the Hamiltonian was given as the sum of eigenvalues En x Pn. Pn is a matrix. He does say at the top of the document that the curly small Es are eigenvalues and En is distinct so my hunch may well be correct.
Again below I'm not quite sure where the Pn in the summation for Ho on the bottom disappears to.
I can follow this bit. It assumes that perturbed and unperturbed eigenkets are in the same direction, but I think that is the idea with the small perturbation. The energy values change but not the ket direction.
So we finally get to write perturbed state in terms of the unperturbed, which confirms my last comment.
More maths to follow to work out the perturbed energies En.
Subscribe to:
Comments (Atom)