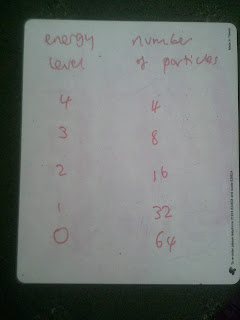
The partition function is used in statistical physics to help define distributions but I've been struggling to work out what it actually is. Here's a speculative attempt. I remembered that if there are large numbers of gas particles with equally stepped energy levels then the distribution should be such that there is a common factor between levels. In the case below, n1/n0 = 0.5, n2/n1=0.5. In other words there is a common probability that a particle will in one level higher. Note that if you add them up, the total number of particles here is 124. N=124
This probability is called the Boltzmann factor and it is given as shown below.I calculated the probabilities of being in any given level above the ground state.
The theory for the Boltzmann distribution calculates the number nj in any given level using the equation shown. Remember that our total number of particles N=124. The summation on the bottom of the equation is the PARTITION FUNCTION. It looks like a summation if Boltzmann factors. (Note that beta is often used in the derivation before it turns out to be -1/kT)
So I added up all of my probabilities. I got 1.9375.
I then used this in the equation and it works in predicting the number on that level. So I am going to tentatively say that I think that the partition function can be thought of as a sum of the individual probabilities for a particle to be on any given level above the ground state.